With the arrival of the Apollo 11 mission’s 45th anniversary, and occasional planning and dreaming about a manned mission to Mars, the role of information technology comes again into focus. The next great mission will include a phalanx of computing resources, sensors, radars, hyper spectral cameras, laser rangefinders, and information fusion visualization and analysis tools to knit together everything needed for the astronauts to succeed. Some of these capabilities will be autonomous, predictive, and knowledgable.
But it all began with the Apollo Guidance Computer or AGC, the rather sophisticated for-its-time computer that ran the trigonometric and vector calculations for the original moonshot. The AGC was startlingly simple in many ways, made up exclusively of NOR gates to implement Arithmetic Logic Unit-like functionality, shifts, and register opcodes combined with core memory (tiny ferromagnetic loops) in both RAM and ROM forms (the latter hand-woven by graduate students).
Using NOR gates to create the entire logic of the central processing unit is guided by a few simple principles. A NOR gate combines both NOT and OR functionality together and has the following logical functionality:
[table id=1 /]
The NOT-OR logic can be read as “if INPUT1 or INPUT2 is set to 1, then the OUTPUT should be 1, but then take the logical inversion (NOT) of that”. And, amazingly, circuits built from NORs can create any Boolean logic. NOT A is just NOR(A,A), which you can see from the following table:
[table id=2 /]
AND and OR can similarly be constructed by layering NORs together. For Apollo, the use of just a single type of integrated circuit that packaged NORs into chips improved reliability.
This level of simplicity has another important theoretical result that bears on the transition from simple guidance systems to potentially intelligent technologies for future Mars missions: a single layer of Boolean functions can only compute simple things. And as you layer on the functions you get increased complexity but complexity that is bounded by the depth of the logical function network. In fact, it can be proved that there are functions that can be represented in a k-depth network that can only be represented in a k-1 depth network if that network has exponentially many hidden units relative to the input size.
This is a startling theoretical discovery and motivates much of the deep learning research: functions for classification of Martian hyper spectral imagery need deep networks precisely because the complexity of the classification task rules out the use of shallower ones. Now mostly we are using artificial neural node simplifications to do this rather than Boolean primitives, but the motivations are the same.
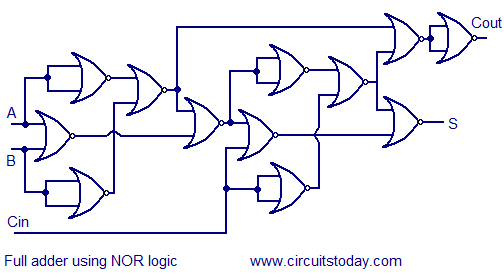
But back to the crawling that predates the running: besides basic logical operations, how can we do something more usefully complex using NORs? Here’s an example logic circuit from circuitstoday.com that shows an adding circuit for adding together bits:
where each of the little half-moons are NORs with their inputs on the left and their outputs to the right. A and B are the inputs while S is the output, and C is the “carry” to the next significant bit. By combining these together, they can add arbitrarily large binary representations of integers with a circuit depth of 7 per 2 bit adder.