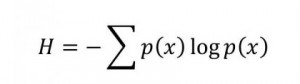Research can flow into interesting little eddies that cohere into larger circulations that become transformative phase shifts. That happened to me this morning between a morning drive in the Northern California hills and departing for lunch at one of our favorite restaurants in Danville.
The topic I’ve been working on since my retirement is whether there are preferential representations for optimal automated inference methods. We have this grab-bag of machine learning techniques that use differing data structures but that all implement some variation on fitting functions to data exemplars; at the most general they all look like some kind of gradient descent on an error surface. Getting the right mix of parameters, nodes, etc. falls to some kind of statistical regularization or bottlenecking for the algorithms. Or maybe you perform a grid search in the hyperparameter space, narrowing down the right mix. Or you can throw up your hands and try to evolve your way to a solution, suspecting that there may be local optima that are distracting the algorithms from global success.
Yet, algorithmic information theory (AIT) gives us, via Solomonoff, a framework for balancing parameterization of an inference algorithm against the error rate on the training set. But, first, it’s all uncomputable and, second, the AIT framework just uses strings of binary as the coded Turing machines, so I would have to flip 2^N bits and test each representation to get anywhere with the theory. Yet, I and many others have had incremental success at using variations on this framework, whether via Minimum Description Length (MDL) principles, it’s first cousin Minimum Message Length (MML), and other statistical regularization approaches that are somewhat proxies for these techniques. But we almost always choose a model (ANNs, compression lexicons, etc.) and then optimize the parameters around that framework. Can we do better? Is there a preferential model for time series versus static data? How about for discrete versus continuous?
So while researching model selection in this framework, I come upon a mention of Shannon’s information theory and its application to quantum decoherence. Of course I had to investigate. And here is the most interesting thing I’ve seen in months from the always interesting Max Tegmark at MIT:
Particles entangle and then quantum decoherence causes them to shed entropy into one another during interaction. But, most interesting, is the quantum Bayes’ theory section around 00:35:00 where Shannon entropy as a classical measure of improbability gets applied to the quantum indeterminacy through this decoherence process.
I’m pretty sure it sheds no particular light on the problem of model selection but when cosmology and machine learning issues converge it gives me mild shivers of joy.