 I am a political independent, though that does not mean that I vote willy-nilly. I have, in fact, been reliably center left for most of my adult life, save one youthfully rebellious moment when I voted Libertarian, more as a statement than a commitment to the principles of libertarianism per se. I regret that vote now, given additional exposure to the party and the kinds of people it attracts. To me, the extremes of the American political system build around radical positions, and the increasingly noxious conspiracy theories and unhinged rhetoric is nothing like the cautious, problem-solving utopia that might make me politically happy, or at least wince less.
I am a political independent, though that does not mean that I vote willy-nilly. I have, in fact, been reliably center left for most of my adult life, save one youthfully rebellious moment when I voted Libertarian, more as a statement than a commitment to the principles of libertarianism per se. I regret that vote now, given additional exposure to the party and the kinds of people it attracts. To me, the extremes of the American political system build around radical positions, and the increasingly noxious conspiracy theories and unhinged rhetoric is nothing like the cautious, problem-solving utopia that might make me politically happy, or at least wince less.
Some might claim I am indifferent. I would not argue with that. In the face of revolution, I would require a likely impossible proof of a better outcome before committing. How can we possibly see into such a permeable and contingent future, or weigh the goods and harms in the face of the unknown? This idea of indifference, as a tempering of our epistemic insights, serves as a basis for an essential idea in probabilistic reasoning where it even has the name, the principle of indifference, or, variously, and in contradistinction with Leibniz’s principle of sufficient reason, the principle of insufficient reason.
So how does indifference work in probabilistic reasoning? Consider a Bayesian formulation: we inductively guess based on a combination of a priori probabilities combined with a posteriori evidences. What is the likelihood of the next word in an English sentence being “is”? Indifference suggests that we treat each word as likely as any other, but we know straight away that “is” occurs much more often than “Manichaeistic” in English texts because we can count words.… Read the rest

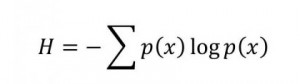 Research can flow into interesting little eddies that cohere into larger circulations that become transformative phase shifts. That happened to me this morning between a morning drive in the Northern California hills and departing for lunch at one of our favorite restaurants in Danville.
Research can flow into interesting little eddies that cohere into larger circulations that become transformative phase shifts. That happened to me this morning between a morning drive in the Northern California hills and departing for lunch at one of our favorite restaurants in Danville.