Tag: solomonoff

A Paradigm of Guessing

Mark DavisLeave a comment

boxesThe most interesting thing I’ve read this week comes from Jurgen Schmidhuber’s paper, Algorithmic Theories of Everything, which should be provocative enough to pique the most jaded of interests. And the quote is from way into the paper:

The first number is 2, the second is 4, the third is 6, the fourth is 8. What is the fifth? The correct answer is “250,” because the nth number is n 5 −5n^4 −15n^3 + 125n^2 −224n+ 120. In certain IQ tests, however, the answer “250” will not yield maximal score, because it does not seem to be the “simplest” answer consistent with the data (compare [73]). And physicists and others favor “simple” explanations of observations.

And this is the beginning and the end of logical positivism. How can we assign truth to inductive judgments without crossing from fact to value, and what should that value system be?… Read the rest

Universal Artificial Social Intelligence

Mark DavisLeave a comment

Continuing to develop the idea that social reasoning adds to Hutter’s Universal Artificial Intelligence model, below is his basic layout for agents and environments:

A few definitions: The Agent (p) is a Turing machine that consists of a working tape and an algorithm that can move the tape left or right, read a symbol from the tape, write a symbol to the tape, and transition through a finite number of internal states as held in a table. That is all that is needed to be a Turing machine and Turing machines can compute like our every day notion of a computer. Formally, there are bounds to what they can compute (for instance, whether any given program consisting of the symbols on the tape will stop at some point or will run forever without stopping (this is the so-called “halting problem“). But it suffices to think of the Turing machine as a general-purpose logical machine in that all of its outputs are determined by a sequence of state changes that follow from the sequence of inputs and transformations expressed in the state table. There is no magic here.

Hutter then couples the agent to a representation of the environment, also expressed by a Turing machine (after all, the environment is likely deterministic), and has the output symbols of the agent consumed by the environment (y) which, in turn, outputs the results of the agent’s interaction with it as a series of rewards (r) and environment signals (x), that are consumed by agent once again.

Where this gets interesting is that the agent is trying to maximize the reward signal which implies that the combined predictive model must convert all the history accumulated at one point in time into an optimal predictor.… Read the rest

Multitudes and the Mathematics of the Individual

Mark DavisLeave a comment

The notion that there is a path from reciprocal altruism to big brains and advanced cognitive capabilities leads us to ask whether we can create “effective” procedures that shed additional light on the suppositions that are involved, and their consequences. Any skepticism about some virulent kind of scientism then gets whisked away by the imposition of a procedure combined with an earnest interest in careful evaluation of the outcomes. That may not be enough, but it is at least a start.

I turn back to Marcus Hutter, Solomonoff, and Chaitin-Kolmogorov at this point.  I’ll be primarily referencing Hutter’s Universal Algorithmic Intelligence (A Top-Down Approach) in what follows. And what follows is an attempt to break down how three separate factors related to intelligence can be explained through mathematical modeling. The first and the second are covered in Hutter’s paper, but the third may represent a new contribution, though perhaps an obvious one without the detail work that is needed to provide good support.

First, then, we start with a core requirement of any goal-seeking mechanism: the ability to predict patterns in the environment external to the mechanism. This is well-covered since Solomonoff in the 60s who formalized the implicit arguments in Kolmogorov algorithmic information theory (AIT), and that were subsequently expanded on by Greg Chaitin. In essence, given a range of possible models represented by bit sequences of computational states, the shortest sequence that predicts the observed data is also the optimal predictor for any future data also produced by the underlying generator function. The shortest sequence is not computable, but we can keep searching for shorter programs and come up with unique optimizations for specific data landscapes. And that should sound familiar because it recapitulates Occam’s Razor and, in a subset of cases, Epicurus’ Principle of Multiple Explanations.… Read the rest

Solomonoff Induction, Truth, and Theism

Mark Davis1 Comment

LukeProg of CommonSenseAtheism fame created a bit of a row when he declared that Solomonoff Induction largely rules out theism, continuing on to expand on the theme:

If I want to pull somebody away from magical thinking, I don’t need to mention atheism. Instead, I teach them Kolmogorov complexity and Bayesian updating. I show them the many ways our minds trick us. I show them the detailed neuroscience of human decision-making. I show them that we can see (in the brain) a behavior being selected up to 10 seconds before a person is consciously aware of ‘making’ that decision. I explain timelessness.

There were several reasons for the CSA community to get riled up about these statements and they took on several different forms:

  • The focus on Solomonoff Induction/Kolmogorov Complexity is obscurantist in using radical technical terminology.
  • The author is ignoring deductive arguments that support theist claims.
  • The author has joined a cult.
  • Inductive claims based on Solomonoff/Kolmogorov are no different from Reasoning to the Best Explanation.

I think all of these critiques are partially valid, though I don’t think there are any good reasons for thinking theism is true, but the fourth one (which I contributed) was a personal realization for me. Though I have been fascinated with the topics related to Kolmogorov since the early 90s, I don’t think they are directly applicable to the topic of theism/atheism.  Whether we are discussing the historical validity of Biblical claims or the logical consistency of extensions to notions of omnipotence or omniscience, I can’t think of a way that these highly mathematical concepts have direct application.

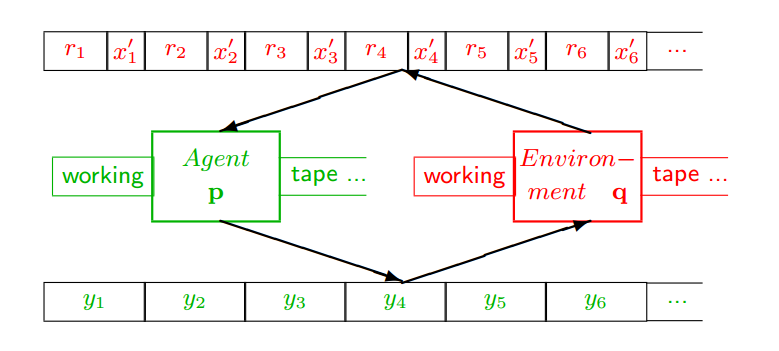
But what are we talking about? Solomonoff Induction, Kolmogorov Complexity, Minimum Description Length, Algorithmic Information Theory, and related ideas are formalizations of the idea of William of Occam (variously Ockham) known as Occam’s Razor that given multiple explanations of a given phenomena, one should prefer the simpler explanation.… Read the rest